Concurso/Encontro Nacional de Programação em Lógica
CeNPL’02
Universidade de
Coimbra / Instituto Politécnico de Coimbra
11-13 de Abril de
2002
Problema nº 7
MIND THE GAP
Introdução
O metropolitano de uma cidade encontra-se parcialmente
representado no mapa da figura 1.
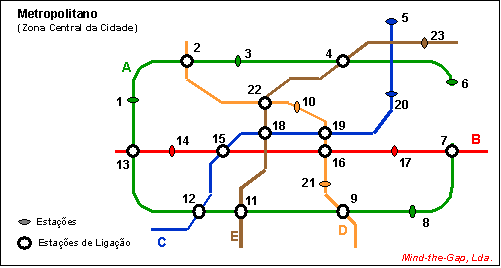
A empresa Mind-theGap,
Lda. que explora o Metro, encomendou-lhe um programa para aconselhar os utentes
sobre quais os melhores percursos a seguir nos seus trajectos. Para já,
pretendem que o programa considere exclusivamente a zona representada no mapa.
Este Metropolitano tem duas peculiaridades: as
composições são novíssimas e deslocam-se a velocidades muito elevadas, pelo que
os tempos de viagem são curtos quando realizados numa única linha; contudo, as
estações são antigas e pouco funcionais, pelo que o tempo necessário para mudar
de linha é muito elevado. Se considerarmos que o custo de uma viagem na zona em
causa é fixo, ou seja, independente da distância percorrida e do número de
linhas utilizado, compreenderemos o pedido feito pela Mind-the-Gap:
“Queremos que o programa forneça ao utente o percurso que lhe permita chegar
ao destino com o número mínimo de mudanças de linha. Nem que o utente tenha que
dar a volta completa à cidade! É melhor do que mudar de linha para encurtar
caminho”.
Tarefa
Escrever um
programa Prolog planner/3 que produza um percurso
de uma estação de origem X a outra estação de destino Y. Um percurso
entre duas estações X e Y pode envolver mais do que uma linha. Quando tal
acontece, é necessário realizar pelo menos uma mudança de linha numa estação
de ligação. Por exemplo, um percurso possível entre as estações 14 e 10 consiste
em efectuar uma viagem na linha B até à estação 16, seguida de outra na linha D até à estação 10.
Os Dados
O programa será invocado através do predicado
planner(
X, Y, Percurso)
que deverá ter os dois primeiros argumentos instanciados com Estações do mapa da Figura 1: X com a estação de partida, Y com a estação de chegada.
A descrição da topologia do Metropolitano é fornecida no ficheiro metro.pl. Neste ficheiro, cada linha é descrita por uma estrutura com a forma linha(Nome, Estacoes), onde Nome identifica a linha e Estacoes é uma lista com as estações da linha.
Por exemplo:
linha('B',
[13,14,15,16,17,7])
Os Resultados
O programa deverá
instanciar Percurso,
o terceiro argumento, com uma lista cujos elementos terão a forma Linha-Muda, significando que o percurso utiliza Linha até à estação Muda.
Esta lista deverá conter um percurso entre X e Y que minimize as mudanças
de linha. Apenas se exige uma solução.
Exemplos:
?-
planner(3, 8, Percurso).
Percurso
= ['A' - 8]
yes
?- planner(6, 10, Percurso).
Percurso
= ['A' - 2,'D' - 10]
yes
?- planner(23, 17, Percurso).
Percurso
= ['E' - 11,'A' - 13,'B' - 17]
yes
Conteúdo do Ficheiro metro.pl:
linha('B', [13,14,15,16,17,7]).
linha('C', [12,15,18,19,20,5]).
linha('D', [2,22,10,19,16,21,9]).
linha('E', [11,18,22,4,23]).